I like to use this as a sort of a crescendo to teaching prime factor decomposition which is itself a very satisfying experience. 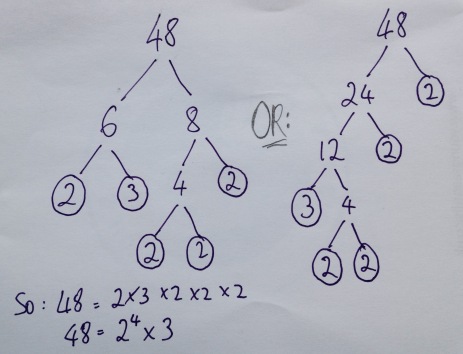
Although it sometimes feels a bit procedural it’s a nice way of:
- Practicing times tables
- Getting to know your primes
- Appreciating the commutativity of multiplication.
Anyway, here’s the trick (everyone needs a calculator in front of them)
- Chose any three digit number. Write it down somewhere.
- Type your number into your calculator and divide by 7.
- Hands up if you got an integer answer. Opportunity here for a nice discussion that we might expect 1 in 7 hands to be up at this point.
- Press clear and divide the same number by 11. Repeat again with 13. Right, now they’ve appreciated that not many numbers are divisible exactly by 7, 11 and 13. Time to blow their minds…
- This time type your 3 digit number into your calculator twice so you have a 6-digit number. e.g.

- Divide by 7. Hands up if you have a whole number. Wow, everyone. Now don’t press clear, but divide by 11. And then 13. Wow. Gets you exactly back to your original 3-digit number.
How much you chose to explain this will depend on the ability of the class, but the points are:
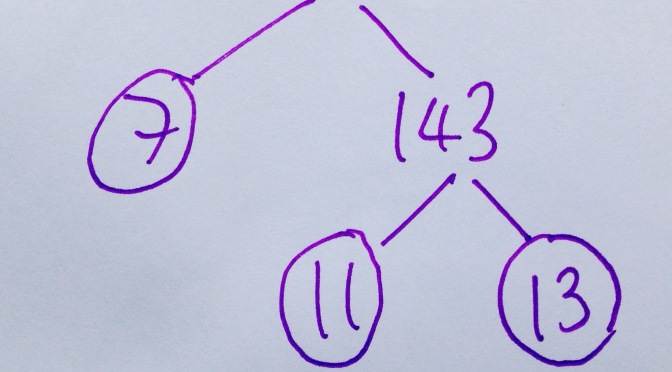
- Whatever 3-digit number you chose, the 6-digit number is 1001 times the 3-digit.
- 1001=7x11x13. Weird but true. And this is why it works.
If your students seem to like it, I always ask them to try it out on their family when they get home. I love the idea that I just might have created a discussion about maths around the dinner table – you never know…

I love it. Going to do an investigation on this with my Y5 class tomorrow.
I suppose you know that 101 x 2-digits gives a 4-digit number which is those 2 digits repeated and better still 10,001 x 4-digits gives an 8-digit number… and so on.
LikeLike
Yes, of course! What a nice way to extend this.
LikeLike
Asking questions are really good thing if you are not understanding anything
completely, but this post provides nice understanding even.
LikeLike